Consider the Bessel Equation of Order $\neq$ 0
Which of These Is the Explicit Formula for the Method

Multiple Choice

Consider the Bessel equation of order .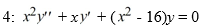
Suppose the method of Frobenius is used to determine a power series solution of the form .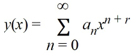
Of this differential equation. Assume a₀ $\neq$ 0.
Which of these is the explicit formula for the coefficients corresponding to the positive root of the indicial equation?

A) $a_{2 n}=0$ and $a_{2 n+1}=(-1) ^{n} \cdot \frac{a_{0} \cdot 4 !}{2^{n+1}(n+1) !(n+4) !}, n \geq 1$
B) $a_{2 n}=0$ and $a_{2 n+1}=(-1) ^{n} \cdot \frac{a_{0} \cdot 4 !}{2^{2 n} n !(n+4) !}, n \geq 1$
C) $a_{2 n+1}=0$ and $a_{2 n}=(-1) ^{n-1} \cdot \frac{a_{0} \cdot 4 !}{2^{n} n !(n+4) !}, n \geq 1$
D) $a_{2 n+1}=0$ and $a_{2 n}=(-1) ^{n} \cdot \frac{a_{0} \cdot 4 !}{2^{2 n} n !(n+4) !}, n \geq 1$