Solved

Consider the Following Third-Order Nonhomogeneous Differential Equation

Question 41

Short Answer

Consider the following third-order nonhomogeneous differential equation:
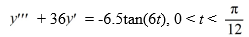
Consider the following third-order nonhomogeneous differential equation: Compute the Wronskian, W(t), for the set of functions Y<sub>1</sub> ,Y<sub>2</sub> , and Y<sub>3</sub> that form a fundamental set and are such that the general solution of the corresponding homogeneous equation + 36 are arbitrary real constants.
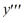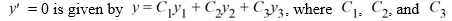Compute the Wronskian, W(t), for the set of functions Y1 ,Y2 , and Y3 that form a fundamental set and are such that the general solution of the corresponding homogeneous equation Consider the following third-order nonhomogeneous differential equation: Compute the Wronskian, W(t), for the set of functions Y<sub>1</sub> ,Y<sub>2</sub> , and Y<sub>3</sub> that form a fundamental set and are such that the general solution of the corresponding homogeneous equation + 36 are arbitrary real constants. + 36 Consider the following third-order nonhomogeneous differential equation: Compute the Wronskian, W(t), for the set of functions Y<sub>1</sub> ,Y<sub>2</sub> , and Y<sub>3</sub> that form a fundamental set and are such that the general solution of the corresponding homogeneous equation + 36 are arbitrary real constants. are arbitrary real constants.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q36: Compute the Wronskian W for the set

Q37: Consider the fourth-order differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"

Q38: On which of these intervals is

Q39: What is the form of a particular

Q40: Solve the following initial value problem:<br> <img

Q42: For which of the following homogeneous

Q43: What is the general solution of

Q44: Compute the Wronskian W for the set

Q45: For which of the following homogeneous

Q46: Compute the Wronskian W for the set