Multiple Choice
What is the general solution of the third-order homogeneous differential equation 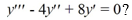 ?
?
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q38: On which of these intervals is
Q39: What is the form of a particular
Q40: Solve the following initial value problem:<br> <img
Q41: Consider the following third-order nonhomogeneous differential equation:<br>
Q42: For which of the following homogeneous
Q44: Compute the Wronskian W for the set
Q45: For which of the following homogeneous
Q46: Compute the Wronskian W for the set
Q47: What is the general solution of
Q48: What is the form of a particular