Multiple Choice
What is the general solution of the third-order homogeneous Cauchy Euler differential equation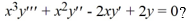
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q44: Compute the Wronskian W for the set
Q45: For which of the following homogeneous
Q46: Compute the Wronskian W for the set
Q47: What is the general solution of
Q48: What is the form of a particular
Q50: What is the general solution of the
Q51: What is the form of a
Q52: Suppose a ninth-order homogeneous linear differential
Q53: What is the form of a
Q54: What is the form of a