Which of the Following Are Solutions to the Homogeneous Second-Order $y_{1}=2 \sin \left(\frac{6}{7} t\right)$

Multiple Choice

Which of the following are solutions to the homogeneous second-order differential equation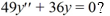
Select all that apply.

A) $y_{1}=2 \sin \left(\frac{6}{7} t\right)$
B) $y_{2}=C\left(\cos \frac{6}{7} t+\sin \frac{6}{7} t\right)$ , where $C$ is any real constant
C) $y_{3}=-2 \cos \left(\frac{7}{6} t\right)$
D) $y_{4}=e^{\frac{6}{7} t}$
E) $y_{5}=C_{1} e^{\frac{6}{7} t}+C_{2} e^{-\frac{6}{7} t}$ where $C_{1}$ and $C_{2}$ are any real constants
F) $y_{6}=5 e^{\frac{7}{6} t}+7 e^{-\frac{7}{6} t}$
G) $y_{7}=\sin \left(\frac{6}{7} t\right) +C$ , where $C$ is any real constant