Multiple Choice
Which of the following is the general solution of the homogeneous second-order differential equation 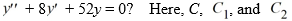
are arbitrary real constants.
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Q14: Which of these is the general
Q15: Consider this initial value problem:<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q16: Suppose a 10-lb object stretches a spring
Q17: Consider this initial value problem:<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q18: Suppose a 160-lb object stretches a spring
Q20: Suppose a 128-lb object stretches a spring
Q21: Consider this second-order nonhomogeneous differential equation:<br><img
Q22: Use variation of parameters to find
Q23: Which of the following functions Y(t)
Q24: Consider the initial value problem<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider