Consider This Second-Order Nonhomogeneous Differential Equation:

Which of the Following

Multiple Choice

Consider this second-order nonhomogeneous differential equation: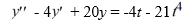

Which of the following is the form of the solution of the corresponding homogeneous differential equation? Here, C₁ and C₂ are arbitrary real constants.

A) $y(t) =C_{1} e^{2 t}(\sin (4 t) +\cos (4 t) ) +C_{2}$
B) $y(t) =C_{1} e^{4 t} \sin (2 t) +C_{2} e^{4 t} \cos (2 t)$
C) $y(t) =C_{1} e^{4 t}(\sin (2 t) +\cos (2 t) ) +C_{2}$
D) $y(t) =C_{1} e^{2 t} \sin (4 t) +C_{2} e^{2 t} \cos (4 t)$