Short Answer
The functions and are defined by the graph below. The dashed graph is and the solid graph is .
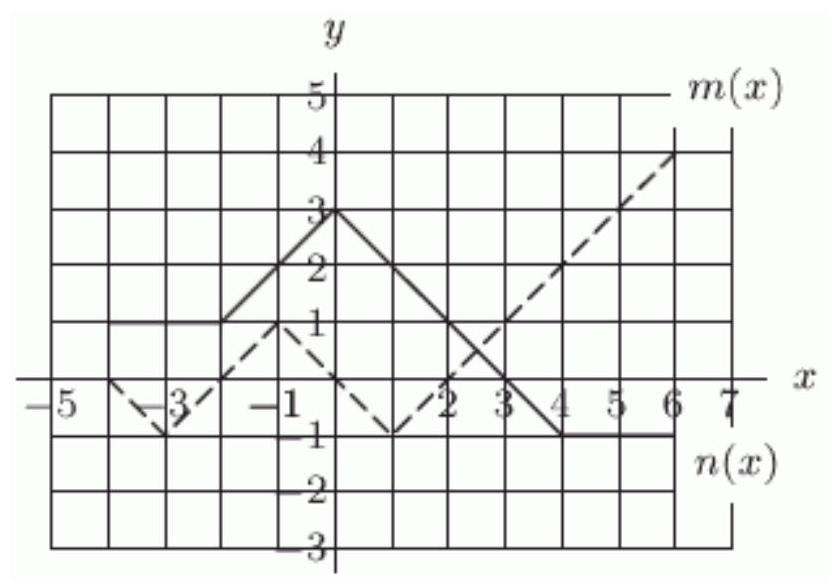
Evaluate .
Correct Answer:

Verified
Correct Answer:
Verified
Q14: Given the graph of <span
Q15: Let <span class="ql-formula" data-value="f(x)=2^{x}"><span class="katex"><span
Q16: Find <span class="ql-formula" data-value="f(f(0))"><span class="katex"><span
Q17: Let <span class="ql-formula" data-value="f(x)=x+1"><span class="katex"><span
Q18: Let <span class="ql-formula" data-value="f(t)"><span class="katex"><span
Q20: Let <span class="ql-formula" data-value="f(x)"><span class="katex"><span
Q21: Let <span class="ql-formula" data-value="f(x)=\frac{4}{2+x}"><span class="katex"><span
Q22: Let <span class="ql-formula" data-value="f"><span class="katex"><span
Q23: The functions <span class="ql-formula" data-value="m(x)"><span
Q24: For <span class="ql-formula" data-value="f(x)=\frac{6}{x}"><span class="katex"><span