Solved

Given the Graph Of ff Below, Solve f(x)=xf(x)=x If There Is More Than One Answer, Enter Them

Question 14

Short Answer

Given the graph of ff below, solve f(x)=xf(x)=x . If there is more than one answer, enter them from least to greatest, separated by semicolons. If there are no solutions, enter "none".
Given the graph of f below, solve f(x)=x . If there is more than one answer, enter them from least to greatest, separated by semicolons. If there are no solutions, enter none .

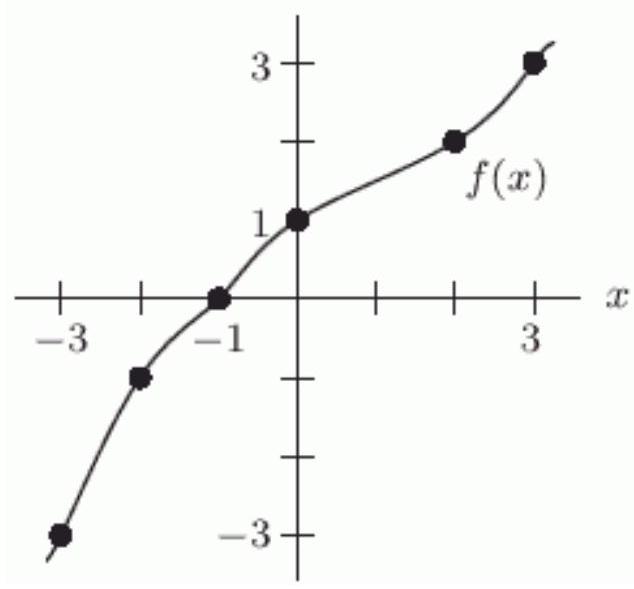
Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q9: The following figure defines a function

Q10: If <span class="ql-formula" data-value="f(x)=x^{2}+2 x"><span

Q11: Given <span class="ql-formula" data-value="f^{-1}(x)=1,300(1.03)^{x}"><span class="katex"><span

Q12: Let <span class="ql-formula" data-value="f(x)=x^{2}+3"><span class="katex"><span

Q13: If <span class="ql-formula" data-value="H(x)=f(g(x))=e^{4 x+2}"><span

Q15: Let <span class="ql-formula" data-value="f(x)=2^{x}"><span class="katex"><span

Q16: Find <span class="ql-formula" data-value="f(f(0))"><span class="katex"><span

Q17: Let <span class="ql-formula" data-value="f(x)=x+1"><span class="katex"><span

Q18: Let <span class="ql-formula" data-value="f(t)"><span class="katex"><span

Q19: The functions <span class="ql-formula" data-value="m(x)"><span