Multiple Choice
Graph the function. Give the domain and range.
- 
A) Domain: ; Range: 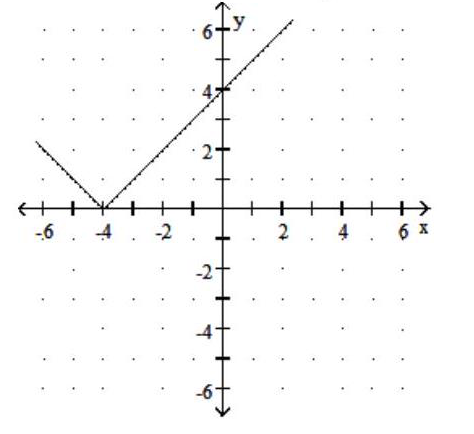
B) Domain: ; Range: 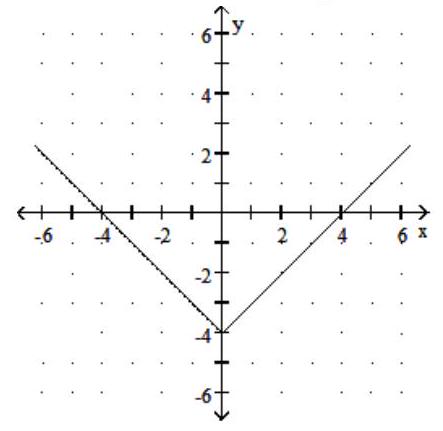
C) Domain: ; Range: 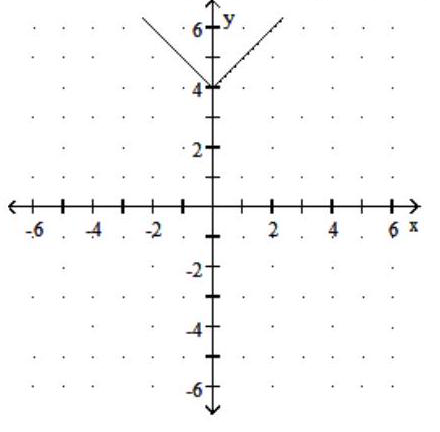
D) Domain: ; Range: 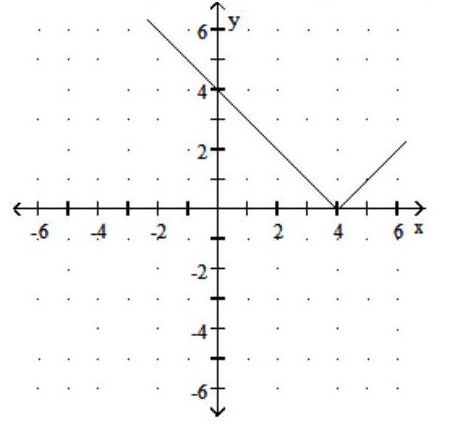
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q26: Solve the problem.<br>-A satellite is to
Q27: Find the equation of a circle
Q28: The hyperbola shown in the calculator-generated
Q29: Choose the equation that matches the
Q30: Graph the step function.<br>-Assume it costs
Q32: Graph the rational function.<br>-f(x) =
Q33: The circle or ellipse shown in
Q34: Graph the circle.<br>- <span class="ql-formula" data-value="(x-6)^{2}+(y-2)^{2}=16"><span
Q35: Graph the system of inequalities.<br>- <span
Q36: Describe the graph of the solution