Solve the Problem $\mathrm{km}$ Determine an Equation for the Ellipse, Where

Multiple Choice

Solve the problem.
-A satellite is to be put into an elliptical orbit around a moon. The moon is a sphere with radius 589 $\mathrm{km}$ . Determine an equation for the ellipse, where $\mathrm{x}$ and $\mathrm{y}$ are measured in $\mathrm{km}$ , if the distance of the satellite from the surface of the moon varies from 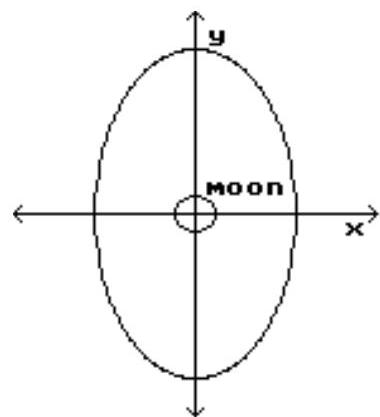$864 \mathrm{~km}$ to $174 \mathrm{~km}$ .

A) $\frac{x^{2}}{1453}+\frac{y^{2}}{763}=1$

B) $\frac{x^{2}}{763^{2}}+\frac{y^{2}}{1453^{2}}=1$

C) $\frac{x^{2}}{864^{2}}+\frac{y^{2}}{174^{2}}=1$

D) $\frac{x^{2}}{174}+\frac{y^{2}}{864}=1$