Multiple Choice
A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is 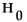
: 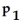
= 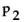
and the alternative is 
: 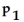
≠ 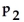
.Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value.
-A university found it retained 25 students out of 352 in 2009 and 36 students out of 334 in 2010.
A) P-value = 0.0455;If there is no difference in the proportions,there is about a 4.55% chance of seeing the observed difference or larger by natural sampling variation.
B) P-value = 0.9545;If there is no difference in the proportions,there is about a 95.45% chance of seeing the observed difference or larger by natural sampling variation.
C) P-value = 0.0455;There is about a 4.55% chance that the two proportions are equal.
D) P-value = 0.091;There is about a 9.1% chance that the two proportions are equal.
E) P-value = 0.091;If there is no difference in the proportions,there is about a 9.1% chance of seeing the observed difference or larger by natural sampling variation.
Correct Answer:

Verified
Correct Answer:
Verified
Q5: A poll reported that 3 out of
Q7: In City A,7420 people are unemployed in
Q18: A two-sample z-test for two population proportions
Q22: You wish to construct a 95% confidence
Q23: In a random sample of 500 people
Q25: Use the given sample data to test
Q32: In Canada,a person with a body mass
Q33: You wish to construct a 90% confidence
Q37: A researcher wished to test the claim
Q51: A Member of Parliament wants to measure