Multiple Choice
Use the following to answer questions :
and are acute angles with tan( ) = 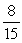 and sec( ) =
and sec( ) =  .
.
-Find sin( - ) .
A) 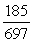
B) 
C) 
D) 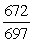
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q2: Use a half-angle identity to rewrite the
Q3: Rewrite in terms of an expression containing
Q4: Evaluate without using a calculator. Answer in
Q5: Simplify without using a calculator. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB3307/.jpg"
Q6: Evaluate without the aid of calculators or
Q7: Verify the equation is an identity by
Q8: Verify that the equation is an identity.
Q9: Find all real solutions. Answer in the
Q10: Use the following to answer questions
Q11: Evaluate using a calculator, keeping in mind