Here Are Plots for Studentized Residuals Against Chest Compare the Regression with the Previous One

Essay

Here are plots for Studentized residuals against Chest. 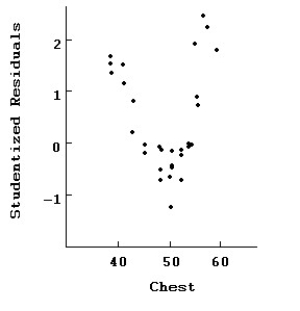Here is the same regression with the two data points with residuals above 2 removed:
Dependent variable is: Weight
30 total bears of which 2 are missing
R-squared = 93.8% R-squared (adjusted)= 93.0%
s = 7.22 with 28 - 4 = 24 degrees of freedom $$\begin{array} { c } & \text { Sum of } & &{ \text { Mean } } \\\text { Source } & \text { Squares } & \text { DF } & \text { Square } & \text { F-ratio } \\\text { Regression } & 21671 & 3 & 7223.67 & 123.23 \\\text { Residual } & 1406.88 & 24 & 58.62 &\end{array}$$ $$\begin{array} { l r c r r } \text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { P-value } \\\text { Intercept } & - 167.52 & 7.47 & - 22.43 & < 0.0001 \\\text { Chest } & 3.01 & 2.98 & 1.01 & 0.3218 \\\text { Length } & 4.05 & 1.53 & 2.65 & 0.0135 \\\text { Sex } & - 2.03 & 2.14 & - 0.95 & 0.3509\end{array}$$ Compare the regression with the previous one.In particular,which model is likely to make the best prediction of weight? Which seems to fit the data better?