Here Are Plots of Data for Studentized Residuals Against Length

Essay

Here are plots of data for Studentized residuals against Length. 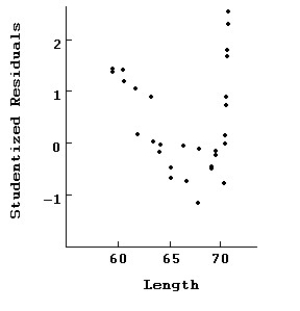Here is the same regression with all of the points at 70 removed.
Dependent variable is: Weight
30 total bears of which 10 are missing
R-squared = 97.8% R-squared (adjusted)= 97.3%
s = 2.96 with 20 - 4 = 16 degrees of freedom $$\begin{array} { l r r r r } & \text { Sum of } & & { \text { Mean } } \\\text { Source } & \text { Squares } & \text { DF } & \text { Square } & \text { F-ratio } \\\text { Regression } & 7455.0 & 3 & 2485 & 238.26 \\\text { Residual } & 166.89 & 16 & 10.43 &\end{array}$$ $$\begin{array} { l r c r r } \text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { P-value } \\\text { Intercept } & - 169.16 & 3.23 & - 52.37 & < 0.0001 \\\text { Chest } & 0.84 & 0.58 & 1.45 & 0.1590 \\\text { Length } & 5.59 & 2.14 & 2.61 & 0.0148 \\\text { Sex } & - 1.19 & 1.98 & - 0.60 & 0.5537\end{array}$$ Compare the regression with the previous one.In particular,which model is likely to make the best prediction of weight? Which seems to fit the data better?