Graph the Quadratic Function $s = - \frac { 1 } { 4 } t ^ { 2 } - t - 1$

Multiple Choice

Graph the quadratic function. Specify the vertex, axis of symmetry, maximum or minimum value, and intercepts. $s = - \frac { 1 } { 4 } t ^ { 2 } - t - 1$

A) vertex: (- 2, 0) ; axis of symmetry: t = - 2; maximum value: 0; t-intercept: - 2; s-intercept: -1.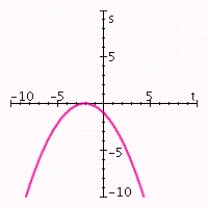
B) vertex: (- 2, 0) ; axis of symmetry: t = - 2; minimum value: 0; t-intercept: - 2; s-intercept: 1.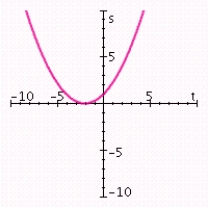
C) vertex: (2, 0) ; axis of symmetry: t = 2; maximum value: 0; t-intercept: 2; s-intercept: -1.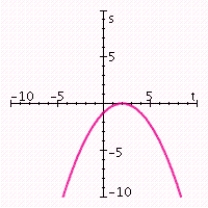
D) vertex: (0,1) ; axis of symmetry: t = 0; maximum value: 1; t-intercept: $\pm 2$ ; s-intercept: 1.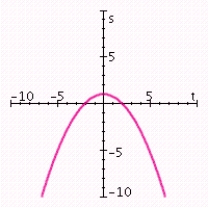
E) vertex: (0, 2) ;axis of symmetry: t = 0; maximum value: 2; t-intercept: $\pm \sqrt { 8 }$ ;s-intercept: 2.