A Triangle Is Inscribed in a Semicircle of Diameter 6R $\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }$

Multiple Choice

A triangle is inscribed in a semicircle of diameter 6R. Show that the smallest possible value for the area of the shaded region is 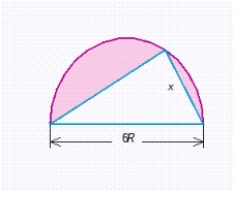$\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }$ . Hint: The area of the shaded region is a minimum when the area of the triangle is a maximum. Find the value of x that maximizes the square of the area of the triangle. This will be the same x that maximizes the area of the triangle.

A) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The area of the triangle is equal to $A ( x ) = \frac { x } { 2 } \sqrt { ( 6 R ) ^ { 2 } - x ^ { 2 } }$ .
The square of the area of the triangle is equal to $( A ( x ) ) ^ { 2 } = 9 R ^ { 2 } x ^ { 2 } - \frac { 1 } { 4 } x ^ { 4 }$ , and the substitution $x ^ { 2 } = t$ will transform this expression into the quadratic function $- \frac { 1 } { 4 } t ^ { 2 } + 9 R ^ { 2 } t ( 1 )$
Since we want to find the maximum value of t, we will substitute the value $t = 18 R ^ { 2 } = x ^ { 2 }$ into the equation. Solving for t gives us the following minimum area of the shaded region: $t = \frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }$ .
B) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The area of the triangle is equal to $A ( x ) = \frac { x } { 2 } \sqrt { ( 6 R ) ^ { 2 } - x ^ { 2 } }$ .
The square of the area of the triangle is equal to $( A ( x ) ) ^ { 2 } = 9 R ^ { 2 } x ^ { 2 } - \frac { 1 } { 4 } x ^ { 4 }$ The substitution $x ^ { 2 } = t$ will transform this expression into the quadratic function $- \frac { 1 } { 4 } t ^ { 2 } + 9 R ^ { 2 } t ( 1 )$
Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is $t = \frac { - b } { 2 a } = 18 R ^ { 2 }$
Substituting the value $t = 18 R ^ { 2 }$ into the equation $t = x ^ { 2 }$ gives us $x ^ { 2 } = 18 R ^ { 2 }$ and consequently $x = 3 R \sqrt { 2 }$ (The negative root can be rejected since the side of a triangle can't be negative) . With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to $\frac { 9 \pi R ^ { 2 } } { 2 } - \frac { 1 } { 2 } x \sqrt { ( 6 R ) ^ { 2 } - x ^ { 2 } }$
Substituting the value $x = 3 R \sqrt { 2 }$ in the equation (2) gives us that the minimum value of the shaded region is equal to $\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }$ .
C) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The square of the area of the triangle is equal to $\frac { 1 } { 4 } 9 R ^ { 2 } x ^ { 2 } + \frac { 1 } { 4 } x ^ { 4 }$ .
The substitution $x ^ { 2 } = t$ will transform this into the quadratic function $\frac { 1 } { 4 } 9 R ^ { 2 } t + \frac { 1 } { 4 } t ^ { 2 }$
Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is $t = \frac { - b } { 2 a } = 9 R ^ { 2 }$
Substituting the value $t = 9 R ^ { 2 }$ into the equation $t = x ^ { 2 }$ gives us $x ^ { 2 } = 9 R ^ { 2 }$ and consequently $x = 3 R$ . With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to $\pi 9 R ^ { 2 } - \frac { 1 } { 2 } x \sqrt { 6 R ^ { 2 } - x ^ { 2 } }$
Substituting the value $x = 3 R$ into the equation (2) , we find that the minimum value of the shaded region is equal to $\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }$ .
D) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle.
The square of the area of the triangle is equal to $A ( x ) = \frac { x } { 2 } \sqrt { ( 6 R ) ^ { 2 } - x ^ { 2 } }$ , which is a quadratic function. The graph of this function will be a parabola opening downward, so we can write the maximum value of this function as: $x ^ { 2 } = \frac { - b } { 2 a } = 18 R ^ { 2 }$
We can then write $x ^ { 2 } = 18 R ^ { 2 }$ as $x ^ { 2 } = 18 R ^ { 2 }$ and calculate the minimum area of the shaded region. Substituting this value into the area equation, we find its minimum area: $\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }$ .
E) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The square of the area of the triangle is equal to $\frac { 1 } { 2 } 9 ^ { 2 } R ^ { 2 } x ^ { 2 } - \frac { 1 } { 4 } x ^ { 4 }$ .
The substitution $x ^ { 2 } = t$ will transform this into the quadratic function $\frac { 1 } { 2 } 9 ^ { 2 } R ^ { 2 } t - \frac { 1 } { 4 } t ^ { 2 }$
Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is $t = \frac { - b } { 2 a } = 3 R ^ { 2 }$
Substituting the value $t = 3 R ^ { 2 }$ into the equation $t = x ^ { 2 }$ gives us $x ^ { 2 } = 3 R ^ { 2 }$ and consequently $x = R \sqrt { 7 }$ . With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to $\frac { \pi 9 R ^ { 2 } } { 4 } - \frac { 1 } { 2 } x \sqrt { 9 R ^ { 2 } - x ^ { 2 } }$
Substituting the value $x = R \sqrt { 7 }$ into the equation (2) , we find that the minimum value of the shaded region is equal to $\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }$ .