Multiple Choice
Graph the parametric equations using the given range for the parameter . Begin with the standard viewing rectangle and then make adjustments, as necessary, so that the graph utilizes as much of the viewing screen as possible. For example, in graphing the circle given by and it would be natural to choose a viewing rectangle extending from -1 to 1 in both the - and -directions. Graph the parametric equations on a graphing utility. Sketch the result. and , (one-quarter of an ellipse)
A) 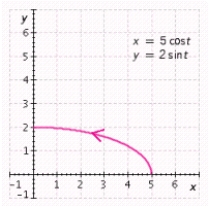
B) 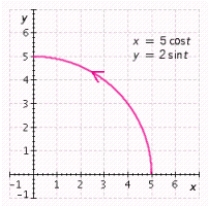
C) 
D) 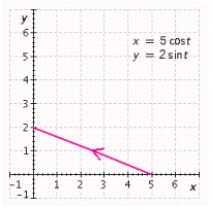
E) 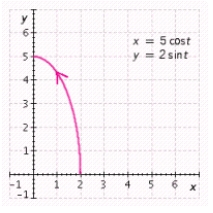
Correct Answer:

Verified
Correct Answer:
Verified
Q15: Refer to the figure. If
Q16: Convert from rectangular to trigonometric form.
Q17: Use the given information to find
Q18: Simplify. <span class="ql-formula" data-value="\frac {
Q19: On a sheet of paper, graph
Q20: Determine the graph that reflects the
Q21: Assume that the coordinates of the
Q22: Convert to rectangular form. <span
Q23: On a sheet of paper, graph
Q24: Carry out the indicated operations.