Question 4
Multiple Choice
The graph of an equation of a sine wave is shown in the figure. Find the amplitude, period, and phase shift. 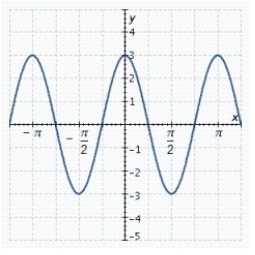
A) amplitude =3, period =π, phaseshift =−4π , y=3sin(2x+2π)
B) amplitude =6, period =π, phaseshift =8π , y=6sin(2x+2π)
C) amplitude =4, period =π, phaseshift =−6π , y=4sin(2x+2π)
D) amplitude =3, period =π, phaseshift =−4π , y=3cos(2x+2π)
E) amplitude =6, period =π, phaseshift =4π , y=6cos(2x+2π)
Correct Answer:

Verified
Unlock this answer now
Get Access to more Verified Answers free of charge

