Three Factories Each Dump Waste Water Containing Three Different Types

Multiple Choice

Three factories each dump waste water containing three different types of pollutants into a river. State regulations require the factories to treat their waste in order to reduce pollution levels. The table shows the possible percent reduction of each pollutant at each site and the cost per ton to process the waste. ​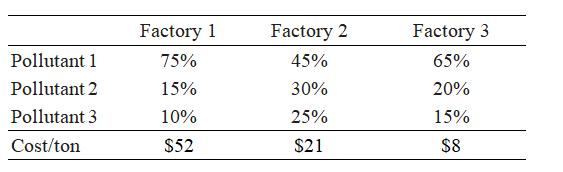

​
If the state requires a reduction of at least 65 tons per day of pollutant 1, at least 40 tons per day of pollutant 2, and at least 20 tons per day of pollutant 3, find the number of tons of waste that must be treated each day at each site so that the state's requirements are satisfied and the treatment costs are minimized. Find the minimum cost.
​
​

A) The minimum cost is $3,190 per day when Factory #2 and Factory #3 each process 110 tons and Factory #1 does not process any.
B) The minimum cost is $2,920 per day when Factory #1 and Factory #2 each process 40 tons and Factory #3 does not process any.
C) The minimum cost is $1,600 per day when Factory #3 process 200 tons, Factory #1 a and Factory #2 do not process any.
D) The minimum cost is $1,540 per day when Factory #1 and Factory #2 each process 20 tons and Factory #3 produces 10 tons.
E) The minimum cost is $2,490 per day when Factory #2 and Factory #3 each process 50 tons and Factory #1 produces 20 tons.