The Millcreek Watershed Area Was Heavily Strip-Mined for Coal During

Multiple Choice

The Millcreek watershed area was heavily strip-mined for coal during the late 1960s. Because of the resulting pollution, the streams cannot support fish. Suppose the cost C of obtaining stream water that contains p percent of the current pollution levels is given by . Because p is the percent of current pollution levels, 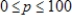. Use the restriction on p and determine a range for C so that an accurate graph can be obtained with a graphing utility. Describe what happens to the cost as p takes on positive values near 0. ​

A) Near p = 0, the cost approaches $3,380.
B) Near p = 0, the cost grows without bound.
C) Near p = 0, the cost approaches $338,000.
D) Near p = 0, cost approaches $0.
E) Near p = 0, the cost becomes negative.