The Linear Programming Problem Has an Unusual Characteristic $$\left( \frac { 20 } { 19 } , \frac { 45 } { 19 } \right)$$

Multiple Choice

The linear programming problem has an unusual characteristic.Select a graph of the solution region for the problem and describe the unusual characteristic.Find the minimum value of the objective function (if possible) and where it occurs. ?
Objective function:
?
Z = 2.5x + y
?
Constraints:
?
X ? 0
Y ? 0
3x + 5y ? 15
?5x + 2y ? 10
?

A) 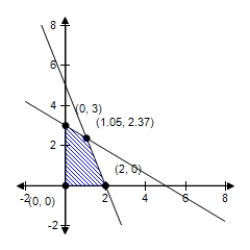Minimum at (0,0) : 0
B) 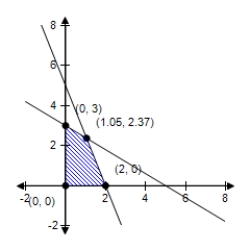Minimum at $$\left( \frac { 20 } { 19 } , \frac { 45 } { 19 } \right)$$ : 5.00
C) ? 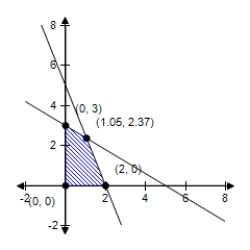Minimum at $$\left( \frac { 20 } { 19 } , 0 \right)$$ : 2.63
D) ? 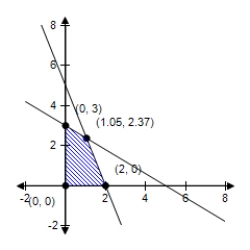No minimum
E) ? 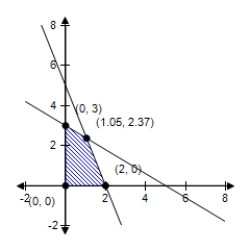Minimum at $\left( \frac { 45 } { 19 } , \frac { 20 } { 19 } \right)$ : 6.97