The Linear Programming Problem Has an Unusual Characteristic

Multiple Choice

The linear programming problem has an unusual characteristic.Select a graph of the solution region for the problem and describe the unusual characteristic.Find the minimum value of the objective function (if possible) and where it occurs. ​
Z = x + 3y
​
Constraints:
​
X ≥ 0
Y ≥ 0
X + 2y ≤ 4
2x + y ≤ 4
​

A) ​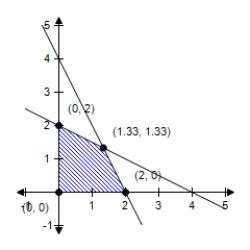 Minimum at (0,2) : 6
B) ​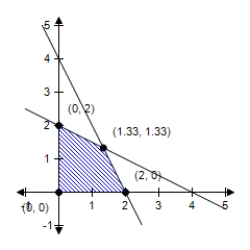 Minimum at (2,0) : 2
C) ​ Minimum at (0,0) : 0
D) ​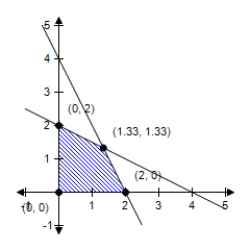 Minimum at (2,2) : 8
E) ​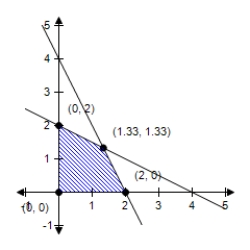 No minimum