Multiple Choice
Use a graphing utility to determine which of the trigonometric functions is equal to the following expression.
A) y = cos x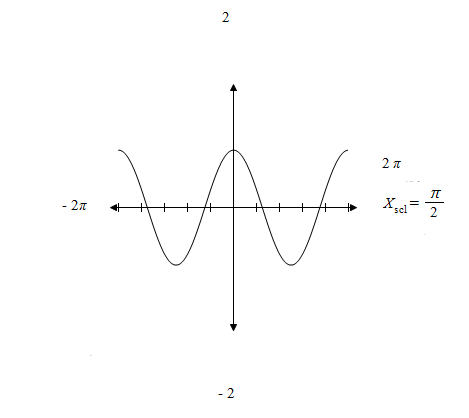
B) y = sin x
2
- 2π 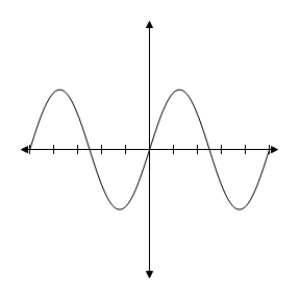
2π
- 2
C) y = csc x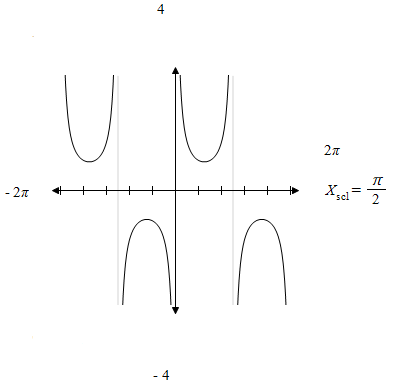
D) y = cot x
4
- 2π 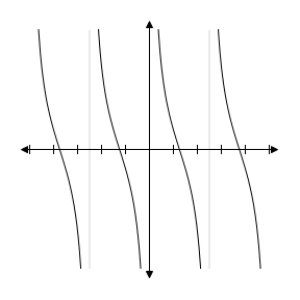
2π
- 4
E) y = tan x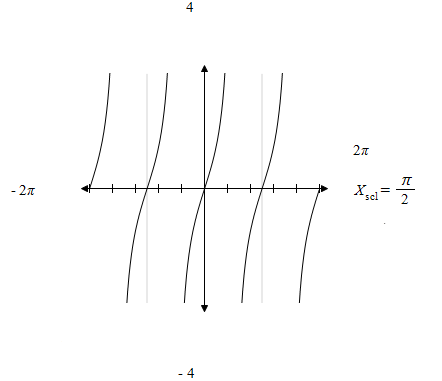
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q7: Rewrite <span class="ql-formula" data-value="\ln |
Q8: Rewrite <span class="ql-formula" data-value="\ln |
Q9: Use the given values to evaluate
Q10: If x = 2 tan θ,use
Q11: If x = 2 tan θ,use
Q13: Use the trigonometric substitution to rewrite
Q14: The forces acting on an object
Q15: Factor;then use fundamental identities to simplify
Q16: Factor;then use fundamental identities to simplify
Q17: By using a graphing utility to