Multiple Choice
Solve the inequality and graph the solution on the real number line.
A) 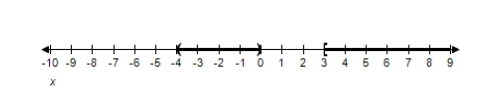
B) 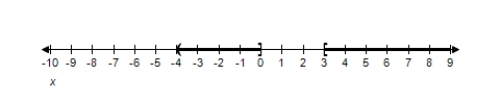
C) 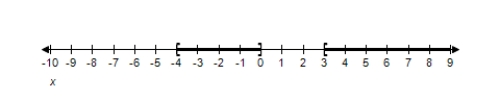
D) 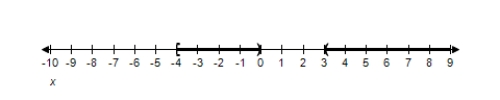
E) 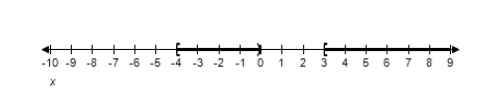
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q11: Find the interval(s)for b such that
Q12: A rectangular parking lot with a
Q13: Determine whether the value of
Q14: Solve the inequality and graph the
Q15: Solve the inequality and write the
Q17: Solve the inequality and graph the
Q18: Solve the inequality and graph the
Q19: Solve the inequality and graph the
Q20: Determine the intervals on which the
Q21: Find the domain of x in