Multiple Choice
Use a graphing utility to graph the equation.Use the graph to approximate the values of x that satisfy the following inequality.
Equation:
Inequality:
A) 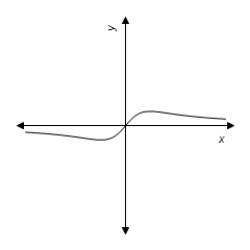
B) 
C) 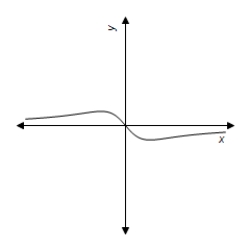
D) 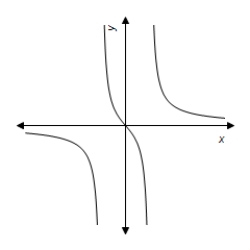
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q25: Solve the inequality and graph the
Q26: Solve the inequality and graph the
Q27: Find the domain of x in
Q28: Find the domain of x in
Q29: Solve the inequality and graph the
Q31: Solve the inequality and graph the
Q32: The numbers N (in millions)of students
Q33: Find the domain of x in
Q34: Solve the inequality and graph the
Q35: Find the key numbers of the