Multiple Choice
Use the given value of k to complete the table for the inverse variation model Plot the points on a rectangular coordinate system.
A)
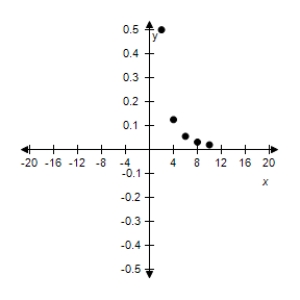
B)
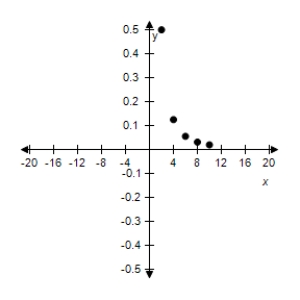
C)
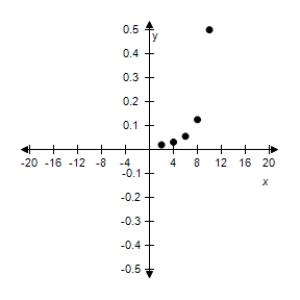
D)
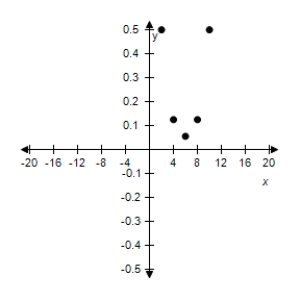
E)
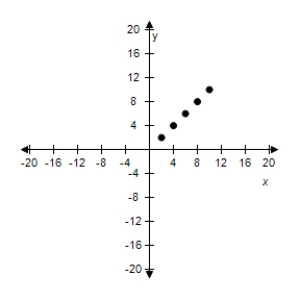
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q25: After determining whether the variation model
Q26: Use the given value of k
Q27: Find a mathematical model representing the
Q28: Determine whether the variation model is
Q29: The simple interest on an investment
Q31: A force of <span class="ql-formula"
Q32: Assume that y is directly proportional
Q33: After determining whether the variation model
Q34: Assume that y is directly proportional
Q35: Use the fact that the resistance of