Multiple Choice
Select the graph of the polar equation using symmetry,zeros,maximum r-values,and any other additional points.
A) Symmetric with respect to ,polar axis,pole Circle with radius
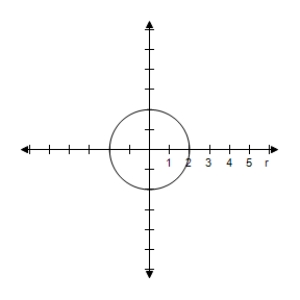
B) Symmetric with respect to ,polar axis,pole Circle with radius
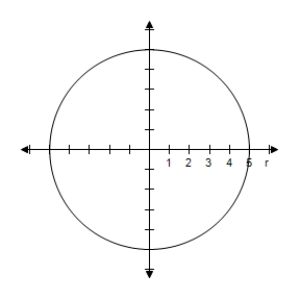
C) Symmetric with respect to ,polar axis,pole Circle with radius
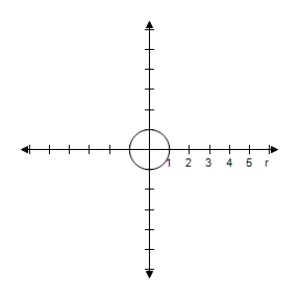
D) Symmetric with respect to ,polar axis,pole Circle with radius
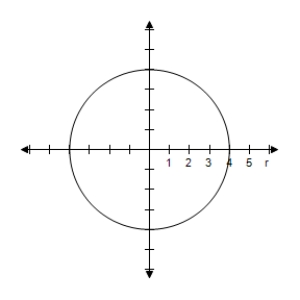
E) Symmetric with respect to ,polar axis,pole Circle with radius
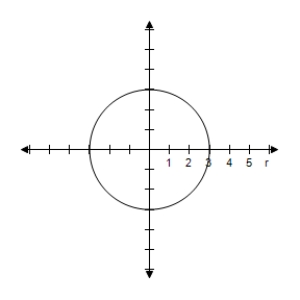
Correct Answer:

Verified
Correct Answer:
Verified
Q39: Select the correct graph of the
Q40: Select the graph of the polar
Q41: Select the graph of the polar
Q42: Select the graph of the polar
Q43: Select the graph of the polar
Q44: Select the correct graph of the
Q45: Select the graph of the polar
Q46: Select the graph of the polar
Q47: Select the graph of <span
Q48: Select the graph of the polar