Multiple Choice
Select the graph of the polar equation using symmetry,zeros,maximum r-values,and any other additional points.
A) Symmetric with respect to the polar axis when
when 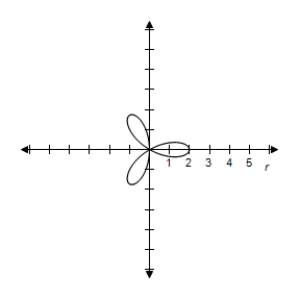
B) Symmetric with respect to the polar axis when
when 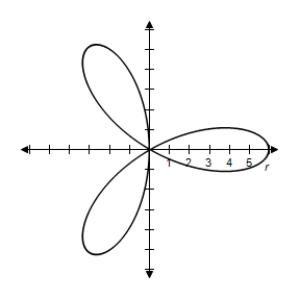
C) Symmetric with respect to the polar axis when
when 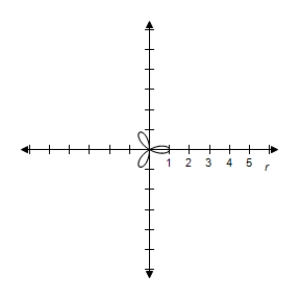
D) Symmetric with respect to the polar axis when
when 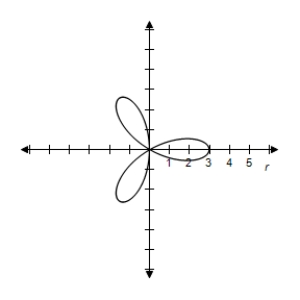
E) Symmetric with respect to the polar axis when
when 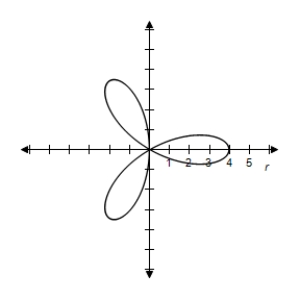
Correct Answer:

Verified
Correct Answer:
Verified
Q23: Select the correct graph of the
Q24: Select the correct graph of the
Q25: Select the graph of the polar
Q26: Select the graph of the equation.
Q27: Select the correct graph of the
Q29: Select the graph of the polar
Q30: Select the correct graph of the
Q31: Select the graph of <span
Q32: Consider the equation <span class="ql-formula"
Q33: Select the graph of the polar