Solved

Select the Correct Graph of the Polar Equation r=9π2r = \frac { 9 \pi } { 2 }

Question 27

Multiple Choice

Select the correct graph of the polar equation.Describe your viewing window.​ r=9π2r = \frac { 9 \pi } { 2 } ​


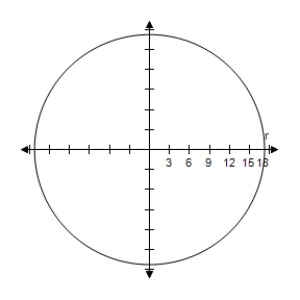
A) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { 9 \pi } { 2 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} B) ​ \begin{array}{l} \theta_{\min }=0 \\ \theta_{\max }=2 \pi \\ \theta_{s t e p}=\pi / 24 \\ X_{\min }=-18 \\ X_{\max }=18 \\ X_{s c l}=3 \\ Y_{\min }=-18 \\ Y_{\max }=18 \\ Y_{s c l}=3 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−18Xmax⁡=18Xscl=3Ymin⁡=−18Ymax⁡=18Yscl=3\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 18 \\X _ { \max } = 18 \\X _ { s c l } = 3 \\Y _ { \min } = - 18 \\Y _ { \max } = 18 \\Y _ { s c l } = 3\end{array}
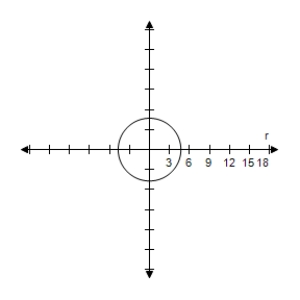
B) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { 9 \pi } { 2 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} B) ​ \begin{array}{l} \theta_{\min }=0 \\ \theta_{\max }=2 \pi \\ \theta_{s t e p}=\pi / 24 \\ X_{\min }=-18 \\ X_{\max }=18 \\ X_{s c l}=3 \\ Y_{\min }=-18 \\ Y_{\max }=18 \\ Y_{s c l}=3 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−18Xmax⁡=18Xscl=3Ymin⁡=−18Ymax⁡=18Yscl=3\begin{array}{l}\theta_{\min }=0 \\\theta_{\max }=2 \pi \\\theta_{s t e p}=\pi / 24 \\X_{\min }=-18 \\X_{\max }=18 \\X_{s c l}=3 \\Y_{\min }=-18 \\Y_{\max }=18 \\Y_{s c l}=3\end{array}
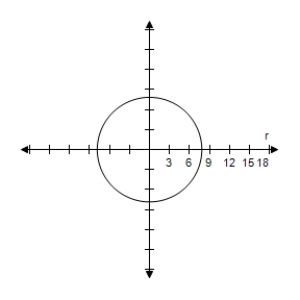
C) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { 9 \pi } { 2 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} B) ​ \begin{array}{l} \theta_{\min }=0 \\ \theta_{\max }=2 \pi \\ \theta_{s t e p}=\pi / 24 \\ X_{\min }=-18 \\ X_{\max }=18 \\ X_{s c l}=3 \\ Y_{\min }=-18 \\ Y_{\max }=18 \\ Y_{s c l}=3 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−18Xmax⁡=18Xscl=3Ymin⁡=−18Ymax⁡=18Yscl=3\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 18 \\X _ { \max } = 18 \\X _ { s c l } = 3 \\Y _ { \min } = - 18 \\Y _ { \max } = 18 \\Y _ { s c l } = 3\end{array}
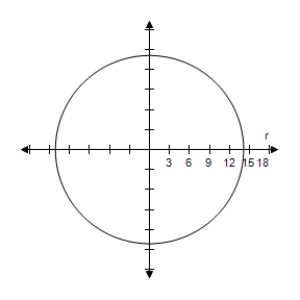
D) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { 9 \pi } { 2 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} B) ​ \begin{array}{l} \theta_{\min }=0 \\ \theta_{\max }=2 \pi \\ \theta_{s t e p}=\pi / 24 \\ X_{\min }=-18 \\ X_{\max }=18 \\ X_{s c l}=3 \\ Y_{\min }=-18 \\ Y_{\max }=18 \\ Y_{s c l}=3 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−18Xmax⁡=18Xscl=3Ymin⁡=−18Ymax⁡=18Yscl=3\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 18 \\X _ { \max } = 18 \\X _ { s c l } = 3 \\Y _ { \min } = - 18 \\Y _ { \max } = 18 \\Y _ { s c l } = 3\end{array}
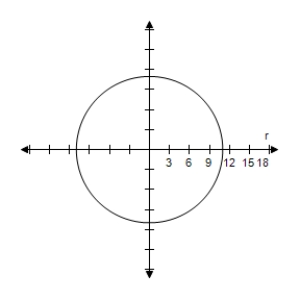
E) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { 9 \pi } { 2 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} B) ​ \begin{array}{l} \theta_{\min }=0 \\ \theta_{\max }=2 \pi \\ \theta_{s t e p}=\pi / 24 \\ X_{\min }=-18 \\ X_{\max }=18 \\ X_{s c l}=3 \\ Y_{\min }=-18 \\ Y_{\max }=18 \\ Y_{s c l}=3 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 18 \\ X _ { \max } = 18 \\ X _ { s c l } = 3 \\ Y _ { \min } = - 18 \\ Y _ { \max } = 18 \\ Y _ { s c l } = 3 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−18Xmax⁡=18Xscl=3Ymin⁡=−18Ymax⁡=18Yscl=3\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 18 \\X _ { \max } = 18 \\X _ { s c l } = 3 \\Y _ { \min } = - 18 \\Y _ { \max } = 18 \\Y _ { s c l } = 3\end{array}

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q22: Select the correct graph of the

Q23: Select the correct graph of the

Q24: Select the correct graph of the

Q25: Select the graph of the polar

Q26: Select the graph of the equation.​

Q28: Select the graph of the polar

Q29: Select the graph of the polar

Q30: Select the correct graph of the

Q31: Select the graph of <span

Q32: Consider the equation <span class="ql-formula"