Solved

Select the Correct Graph of the Polar Equation r=π4r = \frac { \pi } { 4 }

Question 7

Multiple Choice

Select the correct graph of the polar equation.Describe your viewing window.​ r=π4r = \frac { \pi } { 4 } ​


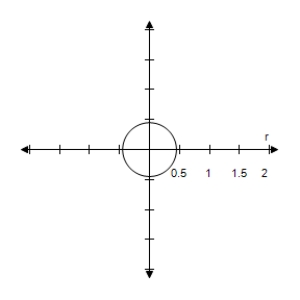
A) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { \pi } { 4 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} B) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−2Xmax⁡=2Xscl=0.5Ymin⁡=−2Ymax⁡=2Yscl=0.5\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 2 \\X _ { \max } = 2 \\X _ { s c l } = 0.5 \\Y _ { \min } = - 2 \\Y _ { \max } = 2 \\Y _ { s c l } = 0.5\end{array}
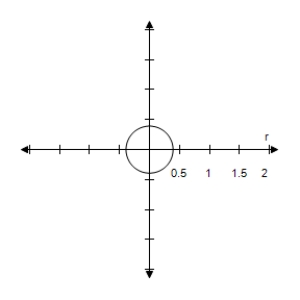
B) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { \pi } { 4 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} B) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−2Xmax⁡=2Xscl=0.5Ymin⁡=−2Ymax⁡=2Yscl=0.5\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 2 \\X _ { \max } = 2 \\X _ { s c l } = 0.5 \\Y _ { \min } = - 2 \\Y _ { \max } = 2 \\Y _ { s c l } = 0.5\end{array}
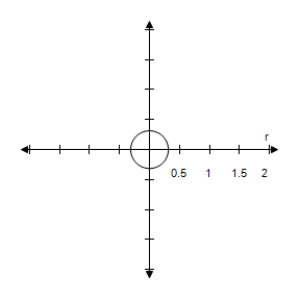
C) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { \pi } { 4 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} B) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−2Xmax⁡=2Xscl=0.5Ymin⁡=−2Ymax⁡=2Yscl=0.5\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 2 \\X _ { \max } = 2 \\X _ { s c l } = 0.5 \\Y _ { \min } = - 2 \\Y _ { \max } = 2 \\Y _ { s c l } = 0.5\end{array}
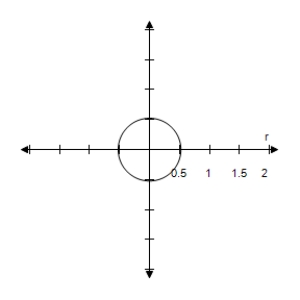
D) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { \pi } { 4 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} B) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−2Xmax⁡=2Xscl=0.5Ymin⁡=−2Ymax⁡=2Yscl=0.5\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 2 \\X _ { \max } = 2 \\X _ { s c l } = 0.5 \\Y _ { \min } = - 2 \\Y _ { \max } = 2 \\Y _ { s c l } = 0.5\end{array}
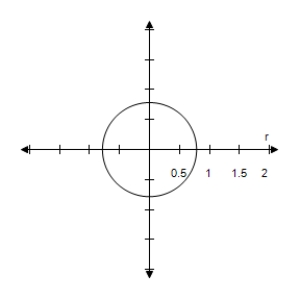
E) ​ Select the correct graph of the polar equation.Describe your viewing window.​ r = \frac { \pi } { 4 } ​ A) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} B) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} C) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} D) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} E) ​ \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 2 \\ X _ { \max } = 2 \\ X _ { s c l } = 0.5 \\ Y _ { \min } = - 2 \\ Y _ { \max } = 2 \\ Y _ { s c l } = 0.5 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−2Xmax⁡=2Xscl=0.5Ymin⁡=−2Ymax⁡=2Yscl=0.5\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 2 \\X _ { \max } = 2 \\X _ { s c l } = 0.5 \\Y _ { \min } = - 2 \\Y _ { \max } = 2 \\Y _ { s c l } = 0.5\end{array}

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q2: Select the graph of the polar

Q3: Select the graph of the polar

Q4: Select the graph of the equation.​

Q5: Select the graph of the equation.​

Q6: Select the correct graph of the

Q8: Select the correct graph of the

Q9: Select the graph of the polar

Q10: Select the graph of the polar

Q11: Select the graph of the polar

Q12: Select the graph of the polar