Multiple Choice
Suppose k, l, and m grow at constant rates given by 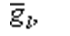 And
And
What is the growth rate of y if
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q35: Until about 12,000 years ago, humans were
Q42: In dynamic economies, it is true that
Q59: If the population of Romania was about
Q60: Assume that both Japan's and the United
Q61: Suppose k and l grow at
Q62: Suppose k, l, and A grow
Q63: Over the past 50 years, Brazil's population
Q66: The relationship between pollution and per capita
Q67: Suppose k, l, and m grow
Q68: The growth rate of any variable