Multiple Choice
Suppose a spring has mass M and spring constant k and let 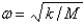 . Suppose that the damping constant is so small that the damping force is negligible. If an external force
. Suppose that the damping constant is so small that the damping force is negligible. If an external force 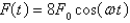 is applied (the applied frequency equals the natural frequency) , use the method of undetermined coefficients to find the equation that describes the motion of the mass.
is applied (the applied frequency equals the natural frequency) , use the method of undetermined coefficients to find the equation that describes the motion of the mass.
A) 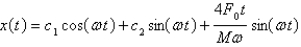
B) 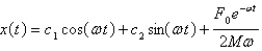
C) 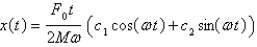
D) 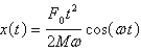
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Q2: Solve the initial-value problem. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Solve
Q3: Solve the differential equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Solve
Q4: Solve the differential equation using the method
Q5: The figure shows a pendulum with length
Q6: Use power series to solve the differential
Q7: Solve the differential equation using the method
Q8: Find a trial solution for the method
Q9: A spring with a mass of <img
Q10: Solve the differential equation using the method
Q11: Solve the differential equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Solve