Solved

Use Spherical Coordinates to Find the Moment of Inertia of the Solid

Question 12

Multiple Choice

Use spherical coordinates to find the moment of inertia of the solid homogeneous hemisphere of radius Use spherical coordinates to find the moment of inertia of the solid homogeneous hemisphere of radius and density 1 about a diameter of its base. A) 195.22 B) 205.13 C) 198.08 D) 213.5 E) and density 1 about a diameter of its base.


A) 195.22
B) 205.13
C) 198.08
D) 213.5
E) Use spherical coordinates to find the moment of inertia of the solid homogeneous hemisphere of radius 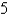and density 1 about a diameter of its base. A) 195.22 B) 205.13 C) 198.08 D) 213.5 E)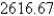

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q7: Evaluate the integral by changing to polar

Q8: Calculate the double integral. Round your answer

Q9: Calculate the double integral. Round your answer

Q10: Find the area of the surface. The

Q11: Evaluate the double integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Evaluate

Q13: A swimming pool is circular with a

Q14: An electric charge is spread over a

Q15: Evaluate the double integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Evaluate

Q16: Evaluate the double integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Evaluate

Q17: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Evaluate the