Solved

Evaluate the Integral by Changing to Polar Coordinates

Question 7

Essay

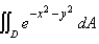
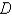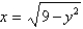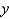Evaluate the integral by changing to polar coordinates. Evaluate the integral by changing to polar coordinates. is the region bounded by the semicircle and the -axis. Evaluate the integral by changing to polar coordinates. is the region bounded by the semicircle and the -axis. is the region bounded by the semicircle Evaluate the integral by changing to polar coordinates. is the region bounded by the semicircle and the -axis. and the Evaluate the integral by changing to polar coordinates. is the region bounded by the semicircle and the -axis. -axis.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q2: Calculate the iterated integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Calculate

Q3: Find the center of mass of the

Q4: Use a double integral to find the

Q5: Find the Jacobian of the transformation. <img

Q6: Evaluate the triple integral. Round your answer

Q8: Calculate the double integral. Round your answer

Q9: Calculate the double integral. Round your answer

Q10: Find the area of the surface. The

Q11: Evaluate the double integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Evaluate

Q12: Use spherical coordinates to find the moment