A Box with an Open Top Is to Be Constructed $b=4$

Multiple Choice

A box with an open top is to be constructed from a rectangular piece of card board with dimensions $b=4$ in. by $a=28$ in. by cutting out equal squares of side $X$ at each corner and then folding up the sides as in the figure. Express the volume $V$ of the box as a function of 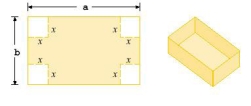$X$ .

A) $V(x) =x^{3}-64 x^{2}+112 x$
B) $V(x) =4 x^{3}+32 x^{2}+196 x$
C) $V(x) =4 x^{3}+64 x^{2}+112 x$
D) $V(x) =x^{3}-32 x^{2}+196 x$
E) $V(x) =4 x^{3}-64 x^{2}+112 x$