Investigators Gave Caffeine to Fruit Flies to See If It

Multiple Choice

Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 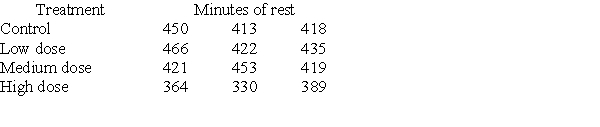A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups. 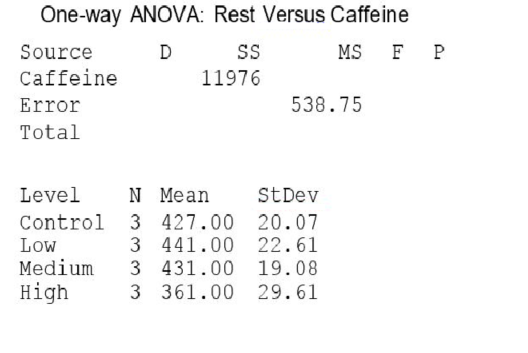The conclusion that you would draw from this test is:

A) accept the null hypothesis; all of the groups have the same mean.
B) fail to reject the null hypothesis; there is no evidence to suggest that the groups have different means.
C) reject the null hypothesis; all of the group means are different.
D) reject the null hypothesis; at least one of the groups has a mean that is different.