Multiple Choice
Let 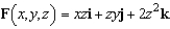 and let S be the surface bounded by
and let S be the surface bounded by 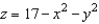 and
and 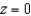 . Verify the Divergence Theorem by evaluating
. Verify the Divergence Theorem by evaluating 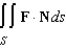 as a surface integral and as a triple integral. Round your answer to two decimal places.
as a surface integral and as a triple integral. Round your answer to two decimal places.
A) 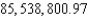
B) 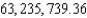
C) 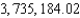
D) 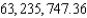
E) 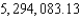
Correct Answer:

Verified
Correct Answer:
Verified
Q5: Use Divergence Theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg"
Q6: Use the Divergence Theorem to evaluate <img
Q7: Use Divergence Theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg"
Q8: Use Divergence Theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg"
Q9: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Evaluate ,
Q11: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Let and
Q12: Use the Divergence Theorem to evaluate <img
Q13: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Let and
Q14: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Evaluate where
Q15: Use the Divergence Theorem to evaluate <img