Solved

Let and Let S Be the Surface Bounded by

Question 13

Multiple Choice

Let Let and let S be the surface bounded by and . Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places. A) B) C) D) E) and let S be the surface bounded by Let and let S be the surface bounded by and . Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places. A) B) C) D) E) and Let and let S be the surface bounded by and . Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places. A) B) C) D) E) . Verify the Divergence Theorem by evaluating Let and let S be the surface bounded by and . Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places. A) B) C) D) E) as a surface integral and as a triple integral. Round your answer to two decimal places.


A) Let and let S be the surface bounded by and . Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places. A) B) C) D) E)
B) Let and let S be the surface bounded by and . Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places. A) B) C) D) E)
C) Let and let S be the surface bounded by and . Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places. A) B) C) D) E)
D) Let and let S be the surface bounded by and . Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places. A) B) C) D) E)
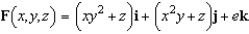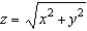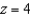E) Let and let S be the surface bounded by and . Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places. A) 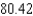B) 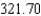C) D) 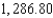E)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q8: Use Divergence Theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg"

Q9: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Evaluate ,

Q10: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Let and

Q11: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Let and

Q12: Use the Divergence Theorem to evaluate <img

Q14: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Evaluate where

Q15: Use the Divergence Theorem to evaluate <img

Q16: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Let and

Q17: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Let and

Q18: Use Divergence Theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg"