Solved

Apply the Trapezoidal Rule and Simpson's Rule to Approximate the Value

Question 1

Multiple Choice

Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. A) The Trapezoidal rule gives and Simpson's rule gives . B) The Trapezoidal rule gives and Simpson's rule gives . C) The Trapezoidal rule gives and Simpson's rule gives . D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. A) The Trapezoidal rule gives and Simpson's rule gives . B) The Trapezoidal rule gives and Simpson's rule gives . C) The Trapezoidal rule gives and Simpson's rule gives . D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives .


A) The Trapezoidal rule gives Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. A) The Trapezoidal rule gives and Simpson's rule gives . B) The Trapezoidal rule gives and Simpson's rule gives . C) The Trapezoidal rule gives and Simpson's rule gives . D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . and Simpson's rule gives Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. A) The Trapezoidal rule gives and Simpson's rule gives . B) The Trapezoidal rule gives and Simpson's rule gives . C) The Trapezoidal rule gives and Simpson's rule gives . D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . .
B) The Trapezoidal rule gives Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. A) The Trapezoidal rule gives and Simpson's rule gives . B) The Trapezoidal rule gives and Simpson's rule gives . C) The Trapezoidal rule gives and Simpson's rule gives . D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . and Simpson's rule gives Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. A) The Trapezoidal rule gives and Simpson's rule gives . B) The Trapezoidal rule gives and Simpson's rule gives . C) The Trapezoidal rule gives and Simpson's rule gives . D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . .
C) The Trapezoidal rule gives Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. A) The Trapezoidal rule gives and Simpson's rule gives . B) The Trapezoidal rule gives and Simpson's rule gives . C) The Trapezoidal rule gives and Simpson's rule gives . D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . and Simpson's rule gives Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. A) The Trapezoidal rule gives and Simpson's rule gives . B) The Trapezoidal rule gives and Simpson's rule gives . C) The Trapezoidal rule gives and Simpson's rule gives . D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . .
D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. A) The Trapezoidal rule gives and Simpson's rule gives . B) The Trapezoidal rule gives and Simpson's rule gives . C) The Trapezoidal rule gives and Simpson's rule gives . D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . .
E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 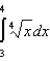A) The Trapezoidal rule gives 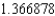and Simpson's rule gives 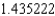. B) The Trapezoidal rule gives 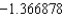and Simpson's rule gives . C) The Trapezoidal rule gives 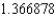and Simpson's rule gives 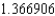. D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives 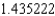. E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives . .

Correct Answer:

verifed

Verified

Related Questions

Q2: Find the smallest n such that the

Q3: Use Simpson's Rule to approximate the value

Q4: Use the Trapezoid Rule to approximate the

Q5: Apply the Trapezoidal Rule and Simpson's Rule

Q6: Find the smallest n such that the

Q7: Use Simpson's Rule to approximate the value

Q8: Apply the Trapezoidal Rule and Simpson's Rule

Q9: Apply the Trapezoidal Rule and Simpson's Rule

Q10: Use Simpson's Rule with <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Use

Q11: Use a computer algebra system and Simpson's