Solved

Let and S Be the Part of the Sphere

Question 1

Multiple Choice

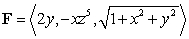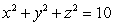Let Let and S be the part of the sphere between the planes and , oriented outward. The integral is equal to which of the following? A) B) C) D) E) and S be the part of the sphere Let and S be the part of the sphere between the planes and , oriented outward. The integral is equal to which of the following? A) B) C) D) E) between the planes Let and S be the part of the sphere between the planes and , oriented outward. The integral is equal to which of the following? A) B) C) D) E) and Let and S be the part of the sphere between the planes and , oriented outward. The integral is equal to which of the following? A) B) C) D) E) , oriented outward. The integral Let and S be the part of the sphere between the planes and , oriented outward. The integral is equal to which of the following? A) B) C) D) E) is equal to which of the following?


A) Let and S be the part of the sphere between the planes and , oriented outward. The integral is equal to which of the following? A) B) C) D) E)
B) Let and S be the part of the sphere between the planes and , oriented outward. The integral is equal to which of the following? A) B) C) D) E)
C) Let and S be the part of the sphere between the planes and , oriented outward. The integral is equal to which of the following? A) B) C) D) E)
D) Let and S be the part of the sphere between the planes and , oriented outward. The integral is equal to which of the following? A) B) C) D) E)
E) Let and S be the part of the sphere between the planes and 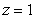, oriented outward. The integral 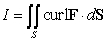is equal to which of the following? A) 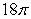B) 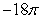C) 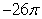D) 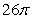E)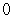

Correct Answer:

verifed

Verified

Related Questions

Q2: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Compute where

Q3: Use Stokes' Theorem to compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q4: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Compute where

Q5: Use Green's Theorem to evaluate the line

Q6: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Compute where

Q7: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Compute where

Q8: Use Green's Theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q9: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate where

Q10: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate where

Q11: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate where