Solved

For Computing the Integral , the Most Efficient Method

Question 23

Multiple Choice

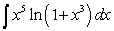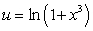For computing the integral For computing the integral , the most efficient method is A) Integration by Parts with and . B) substitution of followed by Integration by Parts. C) Integration by Parts, twice. D) Integration by Parts with and . E) None of the methods covered so far is efficient in computing this integral. , the most efficient method is


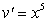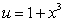A) Integration by Parts with For computing the integral , the most efficient method is A) Integration by Parts with and . B) substitution of followed by Integration by Parts. C) Integration by Parts, twice. D) Integration by Parts with and . E) None of the methods covered so far is efficient in computing this integral. and For computing the integral , the most efficient method is A) Integration by Parts with and . B) substitution of followed by Integration by Parts. C) Integration by Parts, twice. D) Integration by Parts with and . E) None of the methods covered so far is efficient in computing this integral. .
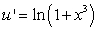B) substitution of For computing the integral , the most efficient method is A) Integration by Parts with and . B) substitution of followed by Integration by Parts. C) Integration by Parts, twice. D) Integration by Parts with and . E) None of the methods covered so far is efficient in computing this integral. followed by Integration by Parts.
C) Integration by Parts, twice.
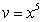D) Integration by Parts with For computing the integral , the most efficient method is A) Integration by Parts with and . B) substitution of followed by Integration by Parts. C) Integration by Parts, twice. D) Integration by Parts with and . E) None of the methods covered so far is efficient in computing this integral. and For computing the integral , the most efficient method is A) Integration by Parts with and . B) substitution of followed by Integration by Parts. C) Integration by Parts, twice. D) Integration by Parts with and . E) None of the methods covered so far is efficient in computing this integral. .
E) None of the methods covered so far is efficient in computing this integral.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q18: To evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="To

Q19: Compute the integrals using the reduction formulas,

Q20: Evaluate the following improper integrals, if they

Q21: The integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The integral

Q22: Which of the following integrals converges?<br>A) <img

Q24: Evaluate the integrals using Integration by Parts,

Q25: Use the substitution <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Use the

Q26: Use the substitution <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Use the

Q27: The time between customers at a checkout

Q28: Evaluate the integral using one or two