Solved

The Integral

Question 21

Multiple Choice

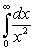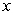The integral The integral : A) diverges since the power of is not less than 1. B) converges since the power of is greater than 1. C) diverges since . D) converges since . E) none of the above :


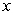A) diverges since the power of The integral : A) diverges since the power of is not less than 1. B) converges since the power of is greater than 1. C) diverges since . D) converges since . E) none of the above is not less than 1.
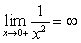B) converges since the power of The integral : A) diverges since the power of is not less than 1. B) converges since the power of is greater than 1. C) diverges since . D) converges since . E) none of the above is greater than 1.
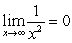C) diverges since The integral : A) diverges since the power of is not less than 1. B) converges since the power of is greater than 1. C) diverges since . D) converges since . E) none of the above .
D) converges since The integral : A) diverges since the power of is not less than 1. B) converges since the power of is greater than 1. C) diverges since . D) converges since . E) none of the above .
E) none of the above

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q16: A cereal-packaging company fills boxes on average

Q17: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate the

Q18: To evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="To

Q19: Compute the integrals using the reduction formulas,

Q20: Evaluate the following improper integrals, if they

Q22: Which of the following integrals converges?<br>A) <img

Q23: For computing the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="For

Q24: Evaluate the integrals using Integration by Parts,

Q25: Use the substitution <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Use the

Q26: Use the substitution <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Use the