Multiple Choice
Consider the following functions. 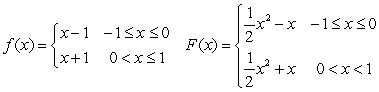 The following statement is correct:
The following statement is correct:
A) 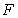 is an antiderivative of
is an antiderivative of 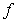 on
on 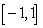 by the Fundamental Theorem of Calculus, Part II.
by the Fundamental Theorem of Calculus, Part II.
B) 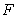 is not an antiderivative of
is not an antiderivative of  on
on 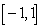 since
since 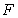 is not differentiable at
is not differentiable at 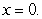
C) 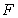 is not an antiderivative of
is not an antiderivative of 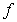 on
on 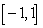 since
since 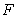 is not the area function of
is not the area function of 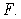
D) If we change the definition of 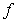 at
at 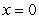 such that
such that 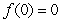 , then
, then  is an antiderivative of
is an antiderivative of 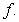
E) 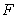 is not an antiderivative of
is not an antiderivative of  on
on 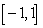 since
since 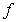 is not differentiable at
is not differentiable at 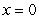 .
.
Correct Answer:

Verified
Correct Answer:
Verified
Q52: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let for
Q53: Which of the following equalities holds for
Q54: Find the general antiderivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"
Q55: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate ."
Q56: Assume that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Assume that
Q58: The substitution <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The substitution
Q59: Use trigonometric identities to evaluate the integral
Q60: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let be
Q61: A population is increasing at a rate
Q62: Use the global extrema of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"