Solved

A Population Is Increasing at a Rate of Individuals

Question 61

Short Answer

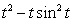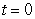A population is increasing at a rate of A population is increasing at a rate of individuals per year. Use the Fundamental Theorem of Calculus Part II to verify that , then find the population after 50 years given that at the population was individuals. individuals per year.
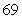Use the Fundamental Theorem of Calculus Part II to verify that A population is increasing at a rate of individuals per year. Use the Fundamental Theorem of Calculus Part II to verify that , then find the population after 50 years given that at the population was individuals. , then find the population after 50 years given that at A population is increasing at a rate of individuals per year. Use the Fundamental Theorem of Calculus Part II to verify that , then find the population after 50 years given that at the population was individuals. the population was A population is increasing at a rate of individuals per year. Use the Fundamental Theorem of Calculus Part II to verify that , then find the population after 50 years given that at the population was individuals. individuals.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q56: Assume that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Assume that

Q57: Consider the following functions. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Consider

Q58: The substitution <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The substitution

Q59: Use trigonometric identities to evaluate the integral

Q60: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let be

Q62: Use the global extrema of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q63: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let ,

Q64: The velocity of a particle is <img

Q65: Evaluate the following integrals using the Fundamental

Q66: Evaluate the following integrals using the Fundamental