Multiple Choice
A rancher removed 200 feet of wire fencing from a field on his ranch. He wants to reuse the fencing to create a rectangular corral into which he will build a 6-foot-wide wooden gate. The dimensions of the corral with the greatest possible area are found using the multivariable functions for the amount of fencing and for the resulting area of the corral: feet is the amount of fencing needed for the specified rectangular corral of width w feet and length l feet. The area of the specified corral is  where w feet is the width and l feet is the length. Write the multivariable function to be maximized.
where w feet is the width and l feet is the length. Write the multivariable function to be maximized.
A) 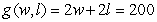
B) 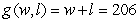
C) 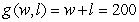
D) 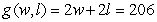
E) 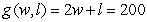
Correct Answer:

Verified
Correct Answer:
Verified
Q32: A model for the elevation above sea
Q33: Locate and classify any critical points. <img
Q34: Milk proteins are sometimes added to sausage
Q35: A model for the elevation above sea
Q36: A nursery sells mulch by the truckload.
Q38: Is the point <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6775/.jpg" alt="Is the
Q39: Test for relative maxima and minima. <img
Q40: The table below gives the number of
Q41: For a region, the percentage of adults
Q42: The table shows the number of days