Solved

Identify the Graph and the Area Bounded by the Curves

Question 51

Multiple Choice

Identify the graph and the area bounded by the curves Identify the graph and the area bounded by the curves on the interval . A) B) C) D) on the interval Identify the graph and the area bounded by the curves on the interval . A) B) C) D) .


A) Identify the graph and the area bounded by the curves on the interval . A) B) C) D) Identify the graph and the area bounded by the curves on the interval . A) B) C) D)
B) Identify the graph and the area bounded by the curves on the interval . A) B) C) D) Identify the graph and the area bounded by the curves on the interval . A) B) C) D)
C) Identify the graph and the area bounded by the curves on the interval . A) B) C) D) Identify the graph and the area bounded by the curves on the interval . A) B) C) D)
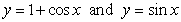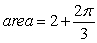
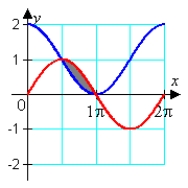
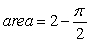
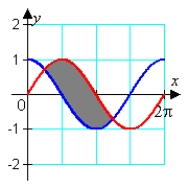
D) Identify the graph and the area bounded by the curves on the interval . A) B) C) D) Identify the graph and the area bounded by the curves on the interval . A) B) C) 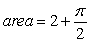D)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q46: Find the volume of the solid with

Q47: Compute the arc length exactly. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"

Q48: The moment of inertia, I, of an

Q49: An anthill is in the shape formed

Q50: Pick the integral that represents a volume

Q52: Find the area between the curves

Q53: A solid is formed by revolving the

Q54: A 30-foot chain weighs 750 pounds and

Q55: Where is the center of mass of

Q56: Starting with the expression for work <img