Solved

Use Lagrange Multipliers to Find the Closest Point on the Given

Question 85

Multiple Choice

Use Lagrange multipliers to find the closest point on the given curve to the indicated point. Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) B) C) D)


A) Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) B) C) D)
B) Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) B) C) D)
C) Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) B) C) D)
D) Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) 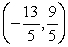B) C) 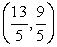D)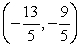

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q80: Find the gradient of the given function

Q81: Compute the directional derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"

Q82: Match the surface to its contour plot.

Q83: Find all first-order partial derivatives. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"

Q84: Find the direction of maximum change of

Q86: Use implicit differentiation to find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"

Q87: Locate all critical points and classify them.

Q88: Show that the indicated limit exists. <img

Q89: Find an equation for the tangent plane

Q90: The number n of gas particles