Solved

Find a Bound on the Error in Approximating the Given

Question 173

Multiple Choice

Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. A) B) C) D)


A) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. A) B) C) D)
B) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. A) B) C) D)
C) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. A) B) C) D)
D) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. 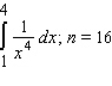A) 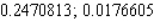B) 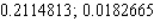C) 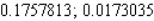D)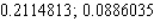

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q168: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6026/.jpg" alt=" A)

Q169: Sales of the latest recording by Brittania,

Q170: Use the table of integrals to find

Q171: Use the table of integrals to find

Q172: Use the table of integrals to find

Q174: Determine whether the given function is a

Q175: Thanks to smaller and more fuel-efficient models,

Q176: Use the formula <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6026/.jpg" alt="Use the

Q177: In a submerged trial run of an

Q178: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6026/.jpg" alt="Find