A Region W In $\mathbb { R } ^ { 3 }$

Essay

A region W in $\mathbb { R } ^ { 3 }$ is described completely by $x \geq 0$ , $y \geq 0$ , $z \geq 0$ , and $x ^ { 2 } + y ^ { 2 } + z ^ { 2 } \leq 4$ .(a) Describe or sketch this region. 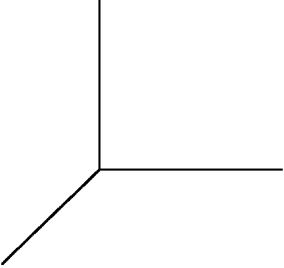(b) Write an integral in rectangular coordinates which gives the volume of W. Do not work out this integral.(c) Write an integral in spherical coordinates which gives the volume of W. Find the volume of W using this integral.